“When I include science in my work, I include it because I want to zoom out,” says Artist Helena Kauppila, a mathematician. She’s fascinated by large, complicated systems, from relationships in financial markets to the arrangements of stars in a galaxy. She also zooms in, exploring the patterns of DNA’s nucleotides in different species’ genes and the patterns and colors one sees while looking at the sky through the branches of deciduous trees in the winter.
Originally, Kauppila used math — specifically stochastic analysis, a type of calculus which describes random events — to explore complex systems. At Columbia University, in New York City, she studied with professors whose work focused on finance. In her dissertation, she described patterns in decisions people make as they spend money and invest it. “For the proofs, I had to deal with lots of theorems regarding infinite spaces and sequences.”
Now Kauppila draws on what she learned at Columbia and at the California Institute of Technology, where she majored in math, in her art. She also finds inspiration in conversations she has with scientists. Using her understanding of random events and the surprising patterns in the systems they make up, she paints objects in outer space. She also paints the sequences of nucleotide bases in the genes that make us all who we are.
From 2009 to 2018, NASA’s Kepler Space Telescope helped scientists see over half a million stars. “Stars are like a Poisson point process,” Kauppila realized after talking with an astronomer. The scientist had explained that stars’ locations in the universe are random — they are not arranged in any sort of simple pattern. “Just because one star is here, you don’t know anything about where the next star is.” The stars can be very far apart and you also have clusters of stars. Therefore “the night sky is an example” of a Poisson point process (a description of objects distributed in space), Kauppila explains.
Her conversation with the astronomer and the images produced by Kepler inspired some of the paintings Kauppila composed for a series she called Distributions.

Helena spent most of her childhood in Finland, where she found math to be both accessible and fun. “If you’re a kid and you want to get into science, maybe you need to go to some science program or science museum for supplies,” she points out. But “for math, you only need pencil and paper — that’s one of the reasons that math is something I got to do a lot as a kid.” She made up her own math games, for instance trying “to guess what the teacher would say next.”
When her family first moved to the United States, Helena did not know English well. But math was “a language on its own” and “the only class I could fully participate in. I would just look at the symbols on the board: those were symbols that I knew!”
Those symbols, which she associated mainly with “games and fun,” later became something she connected with complex systems — “something that could help me understand how the world works.” But many of Kauppila’s friends and family members did not understand her passion for math and it was difficult and an interesting challenge to help them make sense of what she studied.
So she turned to art, with the project of helping non-mathematicians understand what she was working on in mind.
I didn’t directly illustrate the math. I was interested in illustrating the mathematician. I wanted to put art next to math to create this connection with a creative process. Math is something done/invented/discovered by humans; it’s a whole process and a world.
Kauppila created an illustrated version of her thesis and invited her friends and family to use it to learn about her work as both an artist and a mathematician.
People really like flipping through it. They start to ask about what it was like to write the thesis. In that sense it was a success. I wanted to create some discussion around making math, being a mathematician, and it worked.
Eventually, Kauppila moved to Berlin, Germany, and began to focus on her painting. One of the series she has created explores the genetic material of different species to show her audience how connected many forms of life are, arising from a common ancestor. The same four bases of nucleotides (adenine, cytosine, guanine, and thymine) make up the DNA of plants like wheat and animals like human beings. In Kauppila’s words, “it is amazing how much diversity one gets out of four letters!”
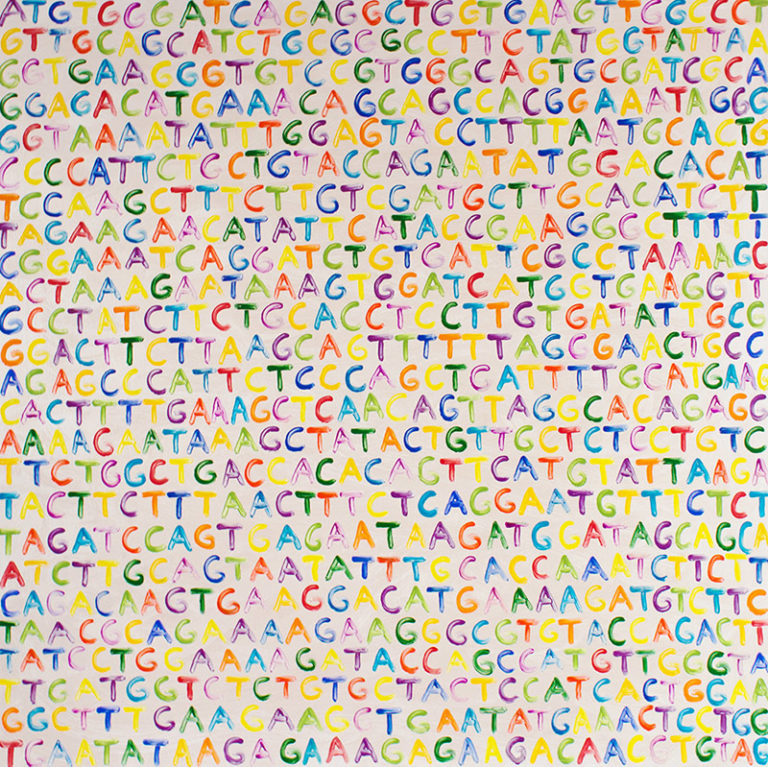

“I’m learning so much about all these different creatures because of this Genetics series,” Kauppila told Math4Science. Then she described the art Japanese pufferfish create on the ocean floor. They arrange sand in intricate patterns for as much as a full week to attract mates. And she pointed out that some viruses embed their genetic codes in the genes of larger species. Scientists now believe that the insertions created by retroviruses led to the development of placenta — the organ with which mammals feed their fetuses.


The “slices of reality I choose to look at come from being a mathematician.” The random mutations in the genetic codes that help cells build individuals within different species and that distinguish those species from each other might be seen as a form of chaos. But within that chaos are beautiful creations and limits creating some sort of order. Kauppila’s work in mathematics and her art help us zoom in and out, better understanding large systems and their beauty and our roles in them.


