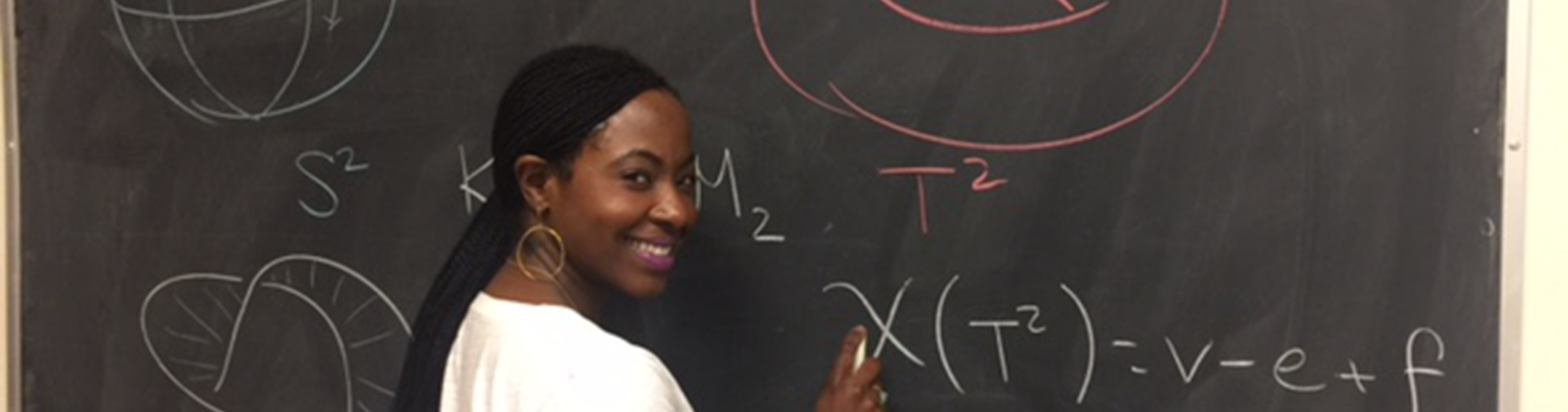Emille Lawrence

At some point, you learned to tell the difference between a triangle (a polygon with three sides), a rectangle (four sides…), and a circle (the set of points that are a certain distance from a particular point). Understanding the differences between those shapes may have been one of your first achievements in a field of mathematics called “geometry.”

Topologist Emille Lawrence focuses on another field of math, one in which a triangle, a rectangle, and a circle are all considered the same shape: a closed, one-dimensional shape with one hole inside of it.  Topologists define a shape by its dimension, by the number of holes that run through it, and by its orientation.

To a topologist, dimensions matter. One dimension describes something with only length — a line segment, for instance, which you can measure with a ruler. Two-dimensional shapes, like the area inside a rectangle, have length and width. And three-dimensional shapes have length, width, and height: a solid pyramid, cone, or prism is a three-dimensional shape.  The number of dimensions of a shape matters in topology, just as it matters to the study of geometry.

But the differences between geometry and topology are great.  For instance, think of a glass — one you might use to drink water. We talk about the “hole” at the top of that glass: the one into which we pour the water.  But if the glass became wet clay or rubber, you could flatten it out to a shape that has no hole at all.  Topologically, the glass has no hole — no opening in the middle that goes through it (if it did, the water would leak out). In other words, topologically, the glass is the same shape as a solid triangle (the area inside a triangle) or the lid of a jar.

Topologists are also interested in the orientation of a shape. Cut a strip of paper, twist it once, and tape or glue the ends together. This creates a möbius strip: if an ant starts walking along the paper at any point and keeps going, it will end up walking along both sides of the strip of paper, over and over. A möbius strip is like an infinite track for the ant. Because the möbius strip has only one side, it is considered non-orientable.  But another two-dimensional shape with a hole in the middle — a flat ring called an annulus– has a front and a back.  You might color the front of an annulus blue, flip it over, and color the back red. Because it is orientable (having two sides), it is a different shape, topologically, than the möbius strip.

Emille grew up in Newnan, Georgia, not far from Atlanta. How did she set out on the path that would have her exploring forms that mush and stretch and change from one recognizable geometric shape to another?

Math was something I was always good at and you know, when you’re good at  something, you tend to want more. As a kid, I was always looking at relationships between numbers and trying to find a little equation.

Digital clocks were my thing: if it were 5:38, I would be in my mind saying “Well, 5 + 3 = 8.” I would impose a relationship on 2:39 — I’d say “Oh, well, 2, 3, 9 … maybe they’re not in the right order, but 3² = 9.” It would be like a little puzzle for me to see if I could find a relationship between the numbers that I was seeing.

Not surprisingly, Lawrence took AP calculus at the end of high school and then majored in mathematics at Spelman College. “I knew that I wanted to major in math and I thought that I wanted to be a math teacher.” Both of Lawrence’s parents were teachers, which inspired her to minor in secondary education. But working at a local high school while studying at Spelman made her see the appeal of teaching at the college level, so she set her sites on graduate school, doing a PhD in mathematics at the University of Georgia.

I went to a smaller liberal arts college [Spelman]. We did not have topology there as a class. The first exposure I had to it was in graduate school, as a first year student. I didn’t immediately like it: it sort of grew on me.

Lawrence arrived in graduate school “wanting to do something in the financial sector,” thinking “I can make some money here.” But gradually she realized that the economic side of math was “kind of boring to me and I saw topology and followed my heart more than my ambition to make money.”

My advisor was also a topologist [Clinton McCrory, at the University of Georgia]. I liked [him] and he made me like the subject even more. When you find a professor or a teacher whom you like and who likes what they’re doing, it just influences you. Their zest and zeal for the subject just spills out.

Topology was very visual: I could draw a picture to get intuition. There’s so much art in math — many people don’t realize that. It’s geometric. There’s a beauty in certain geometric objects you can’t help but notice — even in things that are naturally occurring in the world. A nautilus shell’s spiral and the way it mimics the Fibonacci sequence.

I enjoyed drawing the spaces [and] struggling with it: everything came to life [in topology]. I realized that “Oh, mathematics doesn’t just have to be about equation crunching. Not just numbers but these spaces, these objects which I can actually visualize and even draw in some cases. I just gravitated towards that aspect of it.

And so Lawrence found herself working on braid groups. You probably have some idea about what a braid is: think of braided hair.  To create a braid, one takes a certain number of strands and crosses them over each other, creating a pattern.

Imagine doing this with strands of cooked spaghetti.

Stand them up next to each other in a line and let them dance around one another. You could imagine they could just tangle all up around themselves, but we don’t want them to do that: we want them to go down, just like the braid of your hair. You don’t want the strands to go back up: they’re just twisting around each other, going in a downward pattern. There are two ends: the top of [the braided strands] and the bottom.

“The stuff that happens in-between” is what interests topologists like Lawrence, who look at the ways the strands of each braid “wind around each other in all sorts of ways.”

In her dissertation, Lawrence compared a torus (a two-dimensional shape with one hole) to a three-strand braid. A torus and a braid don’t look very much alike.  But if one focuses on holes and surfaces (as topologists do), a torus with an extra puncture in it becomes similar, in certain ways, to a simple braid. Lawrence found that the two shapes could teach her about each other.

These days, Lawrence works on spatial graphs at the University of San Francisco. “I’m thinking about how the graph is sitting in S3…a three-dimensional sphere.” She looks at different embeddings — different ways of putting a graph (for instance, a triangle) in a given space. And she categorizes these different embeddings into groups. “I’m classifying the topological symmetry groups of a certain abstract graph — the symmetry part is ways of embedding the graph in space but keeping it somewhat the same, embedding it in a symmetric way.”

Does topology intrigue you? Lawrence suggests that you read the science fiction novel Flatland, by Edwin Abbott, and also check out Jeffrey Weeks’s book The Shape of Space, in which he explores the shape of our universe.