How can a triangle help mathematicians predict how likely a driver is to choose any one of three different paths to her destination? Which kind of triangle best models that situation? And what does this have to do with computers? Read on to find out.
Applied Mathematician Fern Hunt uses probability to help us better understand how computers work, how information and disease spread, and patterns in certain kinds of bacteria. The mathematical tools she applies to her work include Markov chains, vertex covers, greedoids, and other complicated ways of analyzing information. Below, you will learn about one of them: the random walk (as well as that triangle model).
Hunt’s interest is in random, or stochastic, processes — things that seem unpredictable. It’s extremely difficult to take the data that scientists, sociologists, and technologists gather and figure out how to make predictions from it. As a mathematician, Hunt studies stochastic processes to help us better understand experimental data and measurements and to suggest new and better ones. Her work is valuable because there is always some mathematical rationale that is needed as part of the process of discovery and measurement.
Fern’s fascination with science began at age nine, when her mother gave her a junior chemistry set. “It was a big hit: I was quite taken with it.” A few years later, her mom gave her the senior set, inspiring her daughter to consider becoming a chemist. In high school, however, the differences between what the mathematical formulas suggested she should find and the results of the chemistry experiments she and her fellow students did frustrated Fern. Perhaps it also planted the seeds for her interest in applied mathematics and probability.
Another frustration Fern confronted as she grew up in New York City was that she was sometimes bullied by other kids at her junior high school. She remembers sitting in class and watching as the clock hand slowly inched towards three o’ clock, thinking about which exit she should use and how fast she needed to run to get out of school safely and home to Manhattan’s Amsterdam Houses. She tells Math4Science that she is “so pleased that [bullying] has become an issue” getting public attention in recent years.

As simple addition, subtraction, multiplication, and division gave way to algebra, Fern began to enjoy math more and more. “I had never really been a big fan of mathematics because it was mostly arithmetic but as it became more and more symbolic and as I came to understand that you could treat whole classes of arithmetic with symbolic notation,” she found herself drawn to the subject. In high school, she read books about math outside of class, including C.D. Old’s Continued Fractions.
At Bryn Mawr, where Hunt went to college, she majored in math. Senior year, she took a class on applied mathematics and read an inspiring book on mathematical biology (Richard Bellman’s Some Vistas of Modern Mathematics: Dynamic Programming, Invariant Imbedding, and the Mathematical Biosciences). Because the ways that math might advance and improve the fields of health sciences and biology had not yet been fully explored, “that appealed to me.”
Hunt’s past work includes a project that looked at computer network traffic. Imagine two towns (really locations in a computer network), each connected to the other by three different routes. Each user (you might think of her or him as a driver going from one town to the other) chooses one of the routes. What’s the probability (what’s the chance) that a user will choose one route over the others? Those of you who have studied probability probably realize that the chances of a user/driver choosing each of the three routes must add up to the number one. “If we’re going to denote an event that’s certain with a probability of one, then these three numbers must add up to one.” Hunt uses information theory entropy to analyze the uncertainty involved in these types of choices.
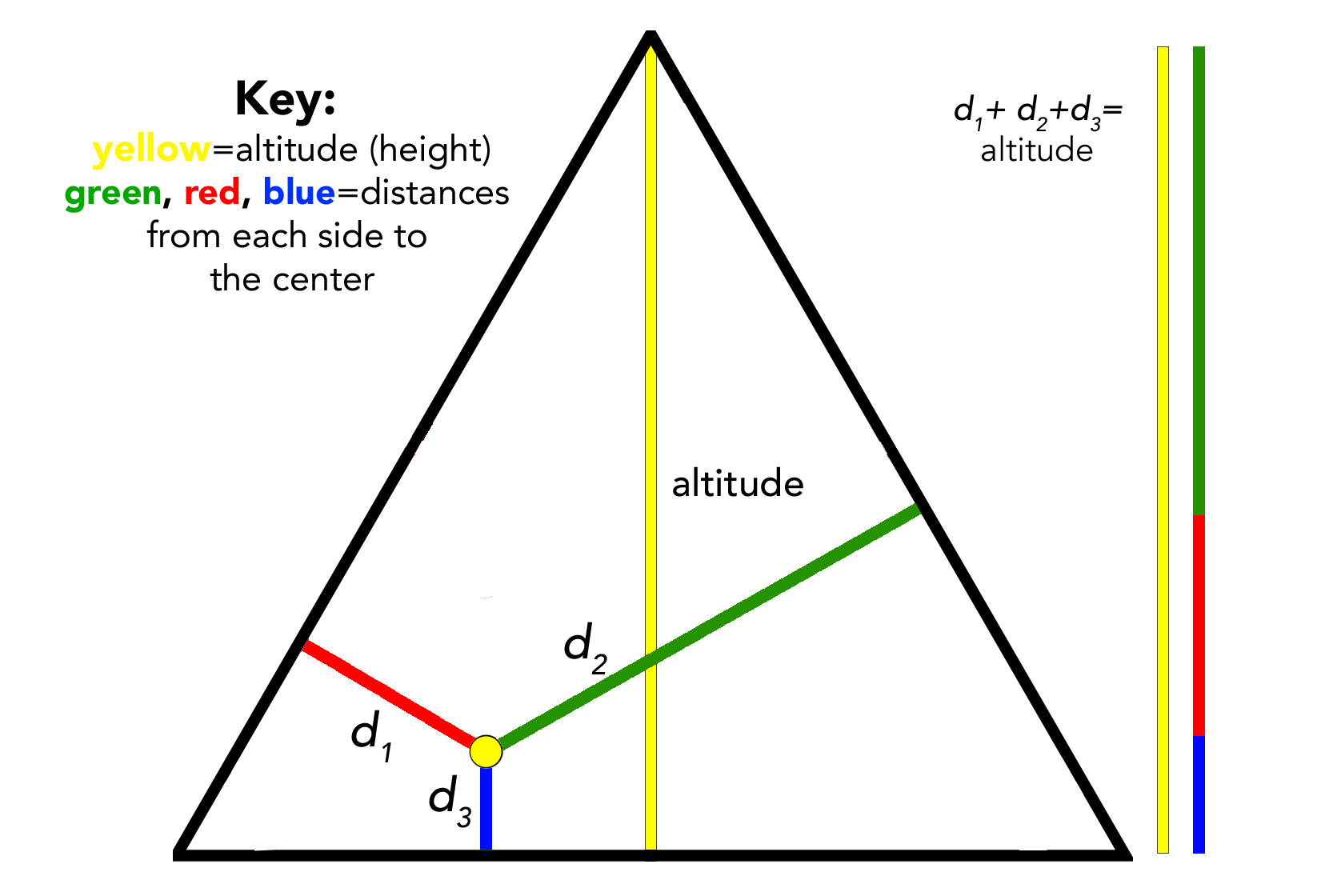
This kind of information theory entropy, says Hunt, can be modeled by the points in an equilateral triangle. Imagine a point somewhere inside the triangle. It is a certain distance from each of the three sides (we might call those distances d1, d2, and d3). If you add those three distances together (d1+ d2+d3), their sum will always be the altitude (height) of the triangle (d1+ d2+d3=1)! Let’s say that the triangle has an altitude of one unit. “We can actually think of these distances as probabilities of choosing routes.” If you think about all of the points inside of the triangle, their distances from the three sides represent all of the possible probabilities of three choices of routes.
Hunt also studies the spread of information in networks, applying a mathematical concept known as “random walk.” This examines the probability of various combinations of positions that a random walker can go to. Her work can help people setting up systems which protect water supplies: sensors located at different positions in the network can communicate as quickly as possible with each other and with people monitoring the system. When something goes wrong (for instance a water main break), sensors can transmit that information to the people who need to shut down certain parts of the system and manage the problems created by the gushing water. Information spread and random walk also have important applications in cyber security, helping us understand the spread of computer viruses. And they are important for public health, allowing public health officials to make more accurate predictions about the spread of epidemics.
Hunt currently works with the National Institute of Standards and Technology (NIST). NIST calibrates standards for measuring instruments and procedures, setting quality control benchmarks for many industries and testing the purity of materials. When a car company buys steel to help it build auto parts or a clothing manufacturer buys cotton or polyester fabric to cut and sew into dresses or suits, they assume the quality (and quantity) of material they are buying is consistent with similar materials they have bought before. NIST’s work is especially important for industrial manufacturing and chemical processing, which require a set of uniform standards and very precise measurements as they make all sorts of products. Thanks to NIST and the work of people like Fern Hunt, manufacturers and their customers can rely on the things they make and buy to work properly under various conditions, such as: under extreme heat, pressure, stretching, etc.
As an applied mathematician for NIST, Hunt’s primary responsibility is conducting mathematical research to support the growth and development of many different fields, from information technology and material sciences to biotechnology. Although she uses different skills in her work, an understanding of statistics and probability as well as the metric system is especially important.

